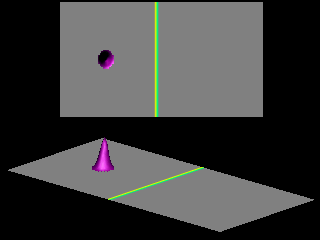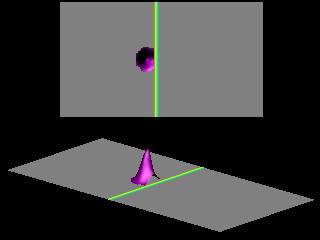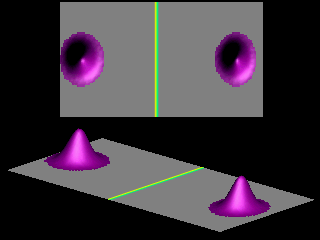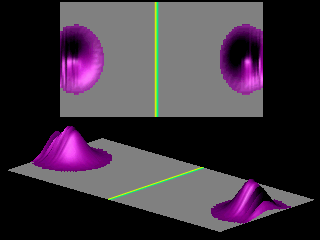
Consider a classical particle (for example a ball) of mass
![]() with a kinetic energy
with a kinetic energy
![]() moving toward a hill of height
moving toward a hill of height
![]() .
The ball rolls up the hill, transforming kinetic energy into potential energy given by
.
The ball rolls up the hill, transforming kinetic energy into potential energy given by
![]() , where
, where
![]() is the acceleration due to gravitation.
If
is the acceleration due to gravitation.
If ![]() the ball will not reach the top. At the point where
the ball will not reach the top. At the point where
![]() the ball reverses its direction and rolls back from the slope.
If
the ball reverses its direction and rolls back from the slope.
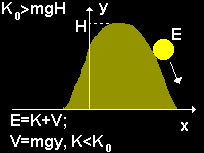
If ![]() the ball will roll over the top of the hill and will run down from the hill on the other side.
the ball will roll over the top of the hill and will run down from the hill on the other side.
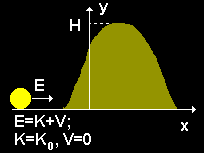
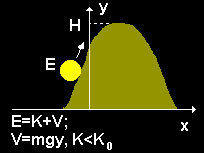
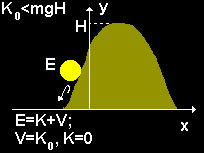
Consider now a particle with energy
![]() approaching a potential step of height
approaching a potential step of height
![]() .
Classically the particle would be reflected by the step.
A quantum particle incident from the left has a nonzero probability for being found to the right of the step.
The animations show the tunneling of Gaussian wave packets through rectangular barriers of height
.
Classically the particle would be reflected by the step.
A quantum particle incident from the left has a nonzero probability for being found to the right of the step.
The animations show the tunneling of Gaussian wave packets through rectangular barriers of height
![]() and width
and width
![]() (central strip).
For visualization purposes, the probability of the transmitted wave (i.e. the wave appearing on the r.h.s. of the strip) has been rescaled.
(central strip).
For visualization purposes, the probability of the transmitted wave (i.e. the wave appearing on the r.h.s. of the strip) has been rescaled.
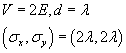
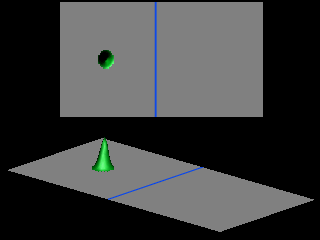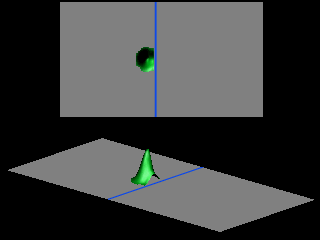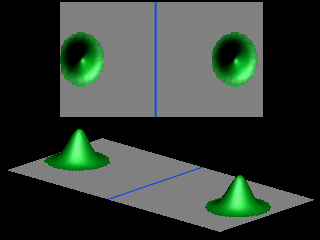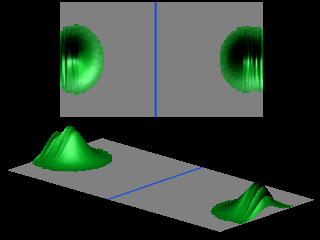
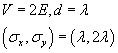
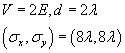
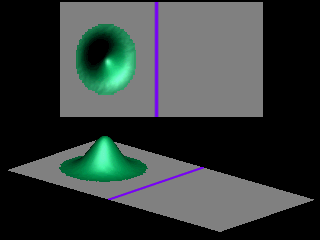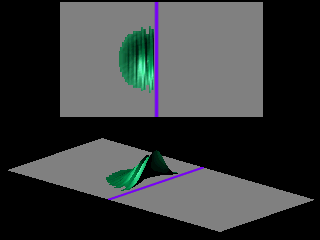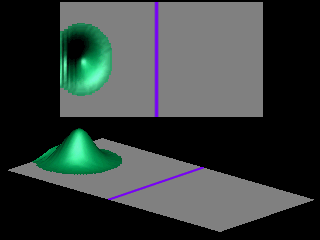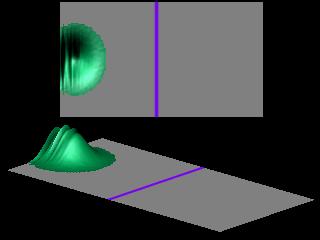
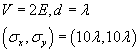

The shape of the transmitted wave packet depends on the width of the initial wave packet.
 The probability for tunneling vanishes exponentially with the thickness of the barrier.
For
The probability for tunneling vanishes exponentially with the thickness of the barrier.
For ![]() and
and
![]() the tunneling probability is less than 0.0000000001.
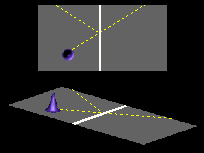
For the potential barrier depicted at the right, the momentum of the particle in the direction parallel to the barrier is conserved.
Therefore the tunneling process does not change the direction of the transmitted wave, as shown in the next animation.
the tunneling probability is less than 0.0000000001.
For the potential barrier depicted at the right, the momentum of the particle in the direction parallel to the barrier is conserved.
Therefore the tunneling process does not change the direction of the transmitted wave, as shown in the next animation.

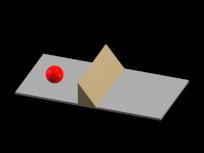
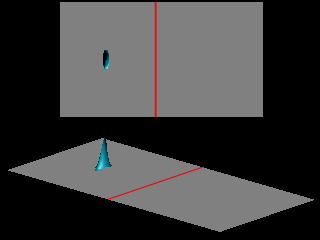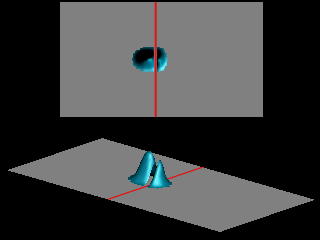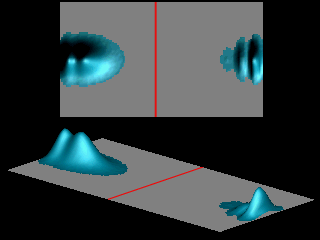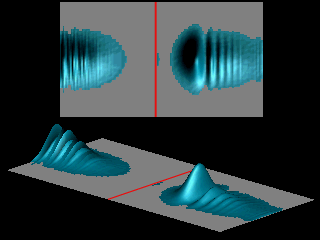
Qualitatively the tunnel effect does not depend on the shape of the potential barrier, as illustrated in the next animation for the case of a triangular barrier.