Black body radiation
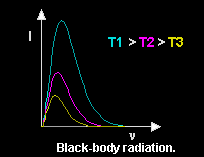When an object is heated, it emits radiation consisting of electromagnetic waves with a broad range of frequencies.
The intensity 
varies with the frequency
of the radiation.
As the temperature increases the dominant frequency increases.
A black body is a body that completely absorbs all the electromagnetic radiation falling on it.
Inside a cavity, e.g. a closed heated oven, the radiation is continuously being absorbed and reemitted by the walls.
A small opening in the cavity will act as a source of radiation. It will give off radiation characteristic of a black body.
Under equilibrium conditions, the dominant frequency of this radiation depends only on the temperature.
The radiation curves were shown to be very similar to Maxwell's velocity distributions of heated gas molecules in a sealed container.
Could the black-body radiation problem be studied in the same way as Maxwell´s ideal gas?
Wien (1894) derived a formula which was confirmed experimentally but there were significant deviations at low frequencies. Lord Rayleigh and Sir Jeans (1900) calculated the energy distribution using the same theoretical assumptions as Maxwell had done with his kinetic theory of gasses. They applied the statistical physics method to waves by analogy with Maxwell´s gas particles using the equipartition of energy, i.e. they assumed that the total energy of radiation is distributed equally among all possible vibration frequencies. BUT in the case of waves there is no limit on the number of modes of vibration that can be excited, because with increasing frequencies (or decreasing wavelengths) the number of waves fitting into the container grows. Consequently the amount of radiation predicted by the theory agreed well at low frequencies but is unlimited and should keep getting stronger and stronger as the temperature is raised and the frequency increases.
Planck´s radiation law (1900): Planck modeled the walls of the cavity as a collection of electric oscillators. He assumed that all frequencies would be present. He also expected that the average frequency increases with increasing temperature since heating the walls causes the oscillators to vibrate faster and faster until thermal equilibrium is reached. The electromagnetic theory could tell everything about the emission, absorption and propagation of the radiation but nothing about the energy distribution at equilibrium. Planck first derived an empirical formula to bridge the gap between Wien's law and Rayleigh Jeans´ law of black-body radiation and then searched for a rigorous derivation of his formula.
At thermal equilibrium, the energy distribution of the radiation matches the energy distribution of the oscillators since the electric oscillators exchange energy with the
radiation in the cavity. Planck postulated for the energy
of an oscillator of frequency
that
where 
is a proportionality constant, nowadays called Planck´s constant.
Hence it is not possible for an oscillator to absorb and emit energy in a continuous range.
It must gain and lose energy discontinuously, in small indivisible units of
, which Planck called energy quanta.
From his quantization condition, Planck derived the thermal energy distribution of the oscillators and the radiation.
Qualitatively, it is understandable how the quantization condition leads to a decrease of the energy at high frequencies:
At high frequencies, even though many modes of vibration are possible, not many are excited because it costs too much energy to make a quantum at a high frequency.